查找与排序

前言

  • 本文主要包括查找算法和经典排序算法两个部分
  • 使用语言：c/c++
  • 仅用于个人学习记录，如有细节错误望理解（欢迎指正）
  • 持续更新中,完整可运行代码见文末
  • 参考https://www.runoob.com/w3cnote/merge-sort.html (归并排序开始)

查找

首先要理解什么是查找。 查找是在相同数据类型的集合中，使用唯一标识（关键字K）来查找数据元素（V）。

平均查找长度 ASL = \(P_1C_1 + P_1C_2 + ......\) 其中\(P_i\)是概率，\(C_i\)是查找第i个元素比较过的次数。 用于分析算法性能。

查找有哪些方法： * 比较式查找法 (1).线性表的查找 (2).树的查找 * 计算式查找法 (1).hash查找

理解以上三点后开始进一步学习具体的查找方法。

比较式查找-基于线性表的查找

顺序查找

存储方式可以是顺序结构，也可以是链式结构 按顺序与关键字比对查找。 

1
2
3
4
5
typedef struct
{
    int key;
    int val;
}KeyValueType;
具体查找代码省略。只需在顺序表中逐个查找对比。

平均查找长度： 设列表中每个数概率相同 P = 1/n。 ASL = \(1/n * (1 + 2 + 3 + ... + n)\) = \((1+n)*n/2 * (1/n)\) = \((1+2)/n\) #### 折半查找 使用折半查找的先前条件：必须是有序排列的顺序表 代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 方便起见不用结构体，直接在int数组里查找，key就是要查找的值x
int BinSearch(int x)
{
    int low = 0,high = n,mid = (high - low)/2 + low;
    while (low < high)
    {
        if (arr[mid] = x)
        {
            return mid;
        }
        else if (arr[mid] < x)
        {
            low = mid + 1;
        }
        else
        {
            high = mid - 1;
        }
        mid = (high - low)/2 + low;
    }
    return -1;
}
平均查找长度： 设每个数的概率一致为P = \(1/n\)。

  • 简单计算方法，可以将长度为n的数组看成n个结点的满二叉树（不妨设刚好满足），这样一来，我们发现，每一次选择一半，就相当于从二叉树底层开始向上攀爬。假设最多选择比较了h次，刚好就是二叉树的高度。 根据满二叉树的性质 \(h = log_2(n+1)\) 换而言之只需要查找h次就一定能找到答案。

  • 公式计算： ASL = \(1/n * Σ_{i=1->n}i*2^{i-1} = (n+1)/n * log_2(n+1) - 1\) 当n足够大时，趋近于\(log_2(n+1)\)

折半查找效率很高，但是要求必须为有序表,导致插入删除很麻烦。 #### 分块查找 通俗来讲，将数组分为多个块，块内数据无序，但是块与块之间有序（如 块0所有元素小于块1的任意元素）。 这是一种结合了折半查找和顺序查找的方法。性能介于两者之间。

模拟一下过程： * 建立索引表，用于指出块的起始位置和最大值。 * 使用折半查找，找到x所在的块，比较方法是比对每个块的最大值maxv。假设块是递增的，那么找到第一个大于等于x的maxv就行。 * 使用顺序查找，在块内逐个比对。

1
2
3
4
5
6
// 注意这里的key有两个
typedef struct
{
    int maxKey;     // 索引区间的最大键值
    int address;    // 索引区间的起始地址（下标）
}Index;

具体查找代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
int BlockSearch(Index *index, int indexLen, int x)
{
    // 先折半查找索引表，找到关键值的索引区间
    int low = 0,high = n,mid = (high - low)/2 + low;
    while (low < high)
    {
        // index.maxKey存储了最大的值 
        if (x == index[mid].maxKey)
        {
            break;
        }
        else if (x < index[mid].maxKey)
        {
            // TODO:这里尤其注意，我们是用最大值进行比较
            // 但是同时，如果我们发现该最大值大于x，我们没有把握说这个x是在找到的这个块，还是前一个。
            // 所以如果high = mid - 1,有可能会错过正确答案。 
            high = mid;
        }
        else
        {
            low = mid + 1;
        }
        mid = (high - low)/2 + low;
    }
    
    // 跳出循环，mid就是要找的索引,就能确定块的start和end 
    int start = index[mid].address, end;
    if (mid == indexLen - 1)
    {
        end = n;
    }
    else
    {
        end = index[mid + 1].address;
    }
    
    // 最后顺序查找返回索引下标 
    for (int i = start; i < end; i++)
    {
        if (x == arr[i])
        {
            return i;
        }
    }
    return -1;
}
平均查找长度： TODO:待计算

基于树的查找

二叉排序树(BST)

二叉排序树就是二叉搜索树或者二叉查找树 根结点上的左子树结点均小于根结点，右子树结点则大于根结点 中序遍历后得到递增有序序列

简单二叉排序树的存储结构 

1
2
3
4
5
6
7
8
9
10
// 用于二叉搜索树 
struct TreeNode {
    int key; // 存储key 
    TreeNode *left;
    TreeNode *right;
    TreeNode() : key(-1), left(nullptr), right(nullptr) {}
    TreeNode(int x) : key(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : key(x), left(left), right(right) {}
};
static TreeNode *root;
##### 创建和插入二叉树排序树 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 创建二叉搜索树（排序树）,使用int作key 
// key是唯一标识不重复 
void CreateBST()
{
    int key;
    TreeNode *bst = nullptr;
    scanf("%d",&key);
    while (key != -1)
    {
        Insert(bst,key);
        scanf("%d",&key);
    } 
}
//递归插入，用于向二叉树中插入某一结点
void Insert(TreeNode *bst,int key)
{
    if (bst == nullptr)
    {
        TreeNode *node = new TreeNode(key);
        bst = node;
    }
    else if (bst->key > key)
        Insert(bst->left,key);
    else 
        Insert(bst->right,key);
}
##### 排序树的查找

1
2
3
4
5
6
7
8
9
10
11
TreeNode* Search(TreeNode *bst,int key)
{
    if (!bst) return nullptr;
    
    if (key == bst->key)
        return bst;
    else if (key < bst->key)
        return Search(bst->left,key);
    else 
        return Search(bst->right,key);		
}
删除
性能

平均查找长度与分支均衡程度有关。 树深度越小，ASL越小。 #### 平衡二叉树（排序树） 又叫做AV树，属于二叉排序树。 * 左子树和右子树高度相差小于等于1 * 平衡因子 = 左 - 右 = {0，1，-1} //TODO:代码 #### B树（排序树）

参考：图解：什么是B树？（心中有 B 树，做人要虚心）一文读懂B-树 - 知乎 (zhihu.com)

B树属于m叉排序树 要求

  • 每个结点最多m棵子树

  • 根结点至少两棵子树

  • 除根结点外非叶子结点至少有一棵子树

  • 所有叶子节点在同一层，称为失败结点，不存储信息，用于分析性能。 存储结构如下 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    #define RANK 10 
    // 用于m叉搜索树 也就是B树 
    struct BTreeNode 
    {
        int keyNum;  // 存储key的数量 
        int key[RANK]; // 因为叶子结点不放信息了，所以只能让父结点存储子结点的信息 
        BTreeNode *p; // 父结点 
        BTreeNode *ptr[RANK]; //子树数组 
        BTreeNode() : keyNum(RANK),p(nullptr)
        {
            for (int i = 0; i < RANK; i ++)
            {
                key[i] = i;
                ptr[i] = nullptr;
            }
        }
    };

  • B树的查找

  • 插入：从根节点开始递归，只能插在叶子结点里，需要判断关键字容量。

1

计算式查找-哈希查找

哈希函数的构造

构造原则
  • 函数便于计算
  • 设关键字为k,f(k)的地址概率一致，减少冲突。 ##### 具体构造方法
  • 数字分析法：事先知道关键字集合，并且关键词比地址码位数多，可以使用,选取均匀的若干位。 //TODO:待补充

构造哈希函数要考虑的东西： * 计算函数的时间 * 关键字长度 * 哈希表大小 * 关键字分布 * 查找频率 #### 处理冲突的方法 * 开放定址法：关键字冲突则以冲突的地址为基础产生新的地址，如此递归，直到不冲突。 * 线性探测再散列：顺序表查看下一个单元 * 二次探测再散列：左右探测 * 伪随机探测再散列：建立伪随机发生器重新给到新地址 * 再哈希算法：不断构造不同哈希函数，直到不冲突 * 链地址法：构造同义词单链表，相同key放到同一个单链表。 整个哈希表存储单链表头指针。 #### 性能分析 除了哈希函数本身，处理冲突的方法以外，填装因子也影响着性能， \(α = n / length\) n表示哈希表元素个数，length则是哈希表长度。

排序算法

插排

  1. 数组存储，边插入，边排序，双重循环

  2. 内循环用将要插入的数从后往前比较，随着已插入的数增加，比较的次数也会增加

时间复杂度为O(n^2)

折半插入排序

  1. 将待插入数组看成有序表（初始为0个元素）
  2. 每插入一个元素，都对有序表循环二分，直到找到合适位置插入
  3. 虽然二分的复杂度只有\(O(log_2n)\),但是移动后续的元素仍然有O(n)，最终复杂度仍然为O（n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 二分插入排序
void BinInsertSort(int n)
{
	int insert;
	for (int i = 0; i < n; i ++)
	{
		int low = 0, high = i,mid = (high - low)/2 + low;
		// 假设边输入边插入，也可以用事先存储的数据 
		cin >> insert;
		
		// 第一个数直接放在第一位 
		if (i == 0) {
			arr[0] = insert;
			continue;
		}
		
		while (low <= high)
		{
			if (arr[mid] > insert)
				high = mid - 1;
			else
				low = mid + 1;
			mid = (high - low)/2 + low;
		}
		// 因为要想插入还需要移动后面的数据
		// 数组中已有i个数,正在插入第i+1个数 
		for (int j = i; j >= low; j --)
			arr[j + 1] = arr[j]; 
		arr[low] = insert;
	}
	// 输出排序结果
	for (int i = 0; i < n; i ++)
	{
		cout<<arr[i]<<' ';
	}
}

表插入排序

使用链表存储进行插入排序

原理与普通插排一样，时间复杂度为O(n^2)

选择排序

简单选择排序

选择出第i小（大）的数。注意区别冒泡排序

复杂度O（n^2)s

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 冒泡,冒泡虽然也是将第i小（大）的数找出来，但是经历了一定次数交换
// n + n-1 + n-2 + ... 
void BubbleSort()
{
    int t[ARRSIZE];
    for (int i = 0; i < ARRSIZE - 1; i ++)
    {
        for (int j = 1; j < ARRSIZE; j ++)
        {
            if (arr[i] > arr[j]) 
            {
                swap(arr[i],arr[j]);
            }
        }
    }
}

// 反观选择排序，则是将第i小（大）的数的下标保存下来，虽然比较次数不变，但是省略了数据交换(swap)的环节
// 简单选择
	void SimpleSelect(int n)
	{
		int k;
		for (int i = 0; i < n - 1; i ++)
		{
			k = i;
			for (int j = i + 1; j < n; j ++)
			{
				if (arr[i] > arr[j])
					k = j;
			}
			if (k != i) 
				swap(arr[i],arr[k]);
		} 
	}

树选择排序

树形结构，因为二叉树的特殊结构，比较次数每次除以2，时间复杂度为O（nlog_2n）。

堆排序

堆排序是基于树选择排序的改进

将数据放在完全二叉树中，根结点>=子结点为大根堆，反之为小根堆。

下图为小根堆

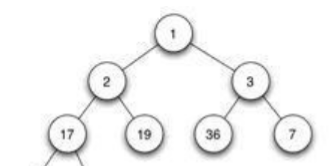
实际使用中将数据放在数组中便于存储 下标从0开始 父结点：\(（i-1）/2\),左子：\(2*i+1\)，右子：\(2 * i+2\)

基本过程

  1. 首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

  2. 将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

  3. 将剩余的n-1个数再构造成大根堆，再将顶端数与当前大根堆末尾位置的数交换，如此反复执行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 堆排序

// 辅助函数
// 让当前堆顶的数下沉，值最小的话就沉入最底 
void createMaxHeap(int start, int end) {
    //建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { //若子节点指标在范围内才做比较
        if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小，选择最大的
            son++;

        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函数
            return;
        else { //否则交换父子内容再继续子节点和孙节点比较
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}
void heapSort(int len) {
    // 从小到大排序，创建大根堆，从最后一个非叶子父结点开始往前
    for (int i = (len-1) / 2; i >= 0; i--)
        createMaxHeap(i, len - 1);
    //先将第一个元素和已经排好的元素前一位做交换，再从新调整(刚调整的元素之前的元素)，直到排序完毕
    for (int i = len - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        createMaxHeap(0, i - 1);
    }
}

时间复杂度为\(O(nlog_2n)\)

归并排序

分解-解决-合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// 归并排序
// 非递归 
template<typename T> // 整數或浮點數皆可使用,若要使用物件(class)時必須設定"小於"(<)的運算子功能
void merge_sort(T arr[], int len) 
{
    T *a = arr;
    T *b = new T[len]; // 存储归并排序后的结果 
    for (int seg = 1; seg < len; seg += seg) 
    {
        for (int start = 0; start < len; start += seg + seg) 
        {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2) // 比较 
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        T *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        for (int i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    delete[] b;
} 	
	
// -------递归---------
void merge_sort_recursive(int arr[], int reg[], int start, int end) 
{
    if (start >= end)
    return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
    reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
    reg[k++] = arr[start1++];
    while (start2 <= end2)
    reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
    arr[k] = reg[k];
}

void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

归并排序时间复杂度O(nlog_2n)

快速排序

  • 从数列中挑出一个元素，称为 "基准"（pivot）;
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序； 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    // 快排，递归
    int Paritition(int A[], int low, int high) {
        int pivot = A[low];
        while (low < high) {
            while (low < high && A[high] >= pivot) {
            --high;
            }
            A[low] = A[high];
            while (low < high && A[low] <= pivot) {
            ++low;
            }
            A[high] = A[low];
        }
        A[low] = pivot;
        return low;
    }

    void QuickSort(int A[], int low, int high)
    {
        if (low < high) {
            int pivot = Paritition(A, low, high);
            QuickSort(A, low, pivot - 1);
            QuickSort(A, pivot + 1, high);
        }
    }

分类排序

基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

可以采用链式和顺序表两种结构存储。 一般使用链式，整体思路是： * 先按照个位进行分类，建立0到9号链表，个位数数值一致则归类到一个链表 * 然后是十位数，百位数进行分类，以此类推，直到排序完成。 时间复杂度为O(d(n+rd)) 显然基数排列适合位数小的序列。 其中d是数的位数， 代码略

github仓库地址：https://github.com/aspect-ux/kanodesu.github.io/tree/main