Ray Tracing(光线追踪)(上)
Why Ray Tracing?
光线追踪和光栅化是两种不同的成像方式,为什么要选择光线追踪呢?
光栅化的局限性在于全局效果的控制: 1. 不能实现软阴影 2. 光照不能反射超过1次(目前技术可行效果不好)
光栅化很快,效果却不好。
相反,光线追踪很慢,但是很精确

Light Rays
Three ideas about light rays(满足三个假设的前提)
- Light travels in straight lines(though this is wrong) 光线沿直线传播
- Light rays do not “collide” with each other if they cross(also wrong) 光线之间无碰撞
- Light rays travel from the light source to the eye(but the physics is in variant under path reversal - reciprocity) (光线可逆性,可以理解为光的方向互逆)
正常情况下,我们的理解是光源打光到物体上,物体反射光照到人眼,根据反射的颜色我们看到物体。
而在光线追踪的过程中,我们在做这样一件事:
从眼睛(相机)出发,投射光线,光线看到的就是人看到的。终点变成了起点,也即上述第三点中的可逆性。
- 记录最近的点 2. 判断这个点是否看得见
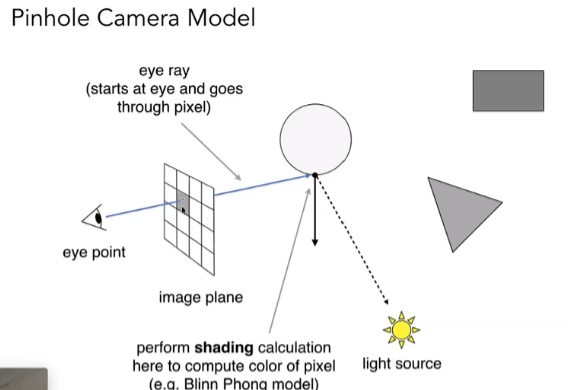
上图中,眼睛就是入射光,指向光源就是出射光,法线确定后,着色就确定了。
光线如何反射多次呢?
Basic Ray Tracing Algorithm(基本光线追踪算法)
Whitted-Style
射线经过递归弹射(recursively bounce),得到了若干弹射点,如果光源能够照射到该点,着色则会add到结果中
eye : primary ray
light: shadow ray
ref: secondary rays
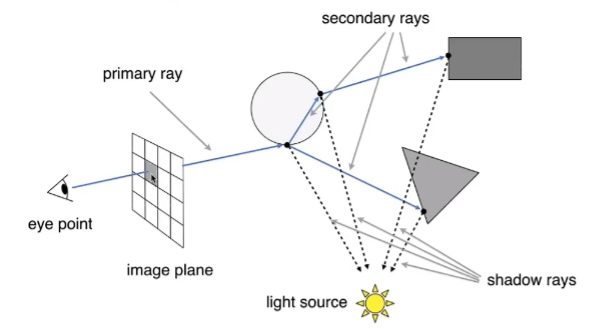
Ray Surface Intersection(求交点)
如何定义光线?一个起点,一个方向,随时间变化
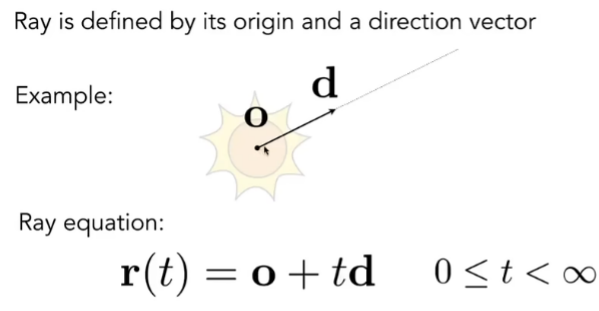
如何求交?
拿光线与球(隐式表面)进行求交来说。满足下图两个式子,联立后得二次方程。
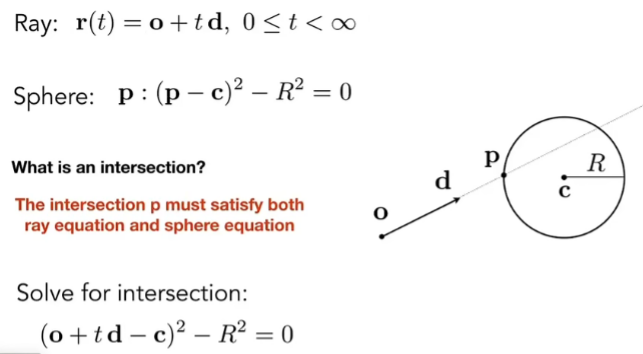
求解后得
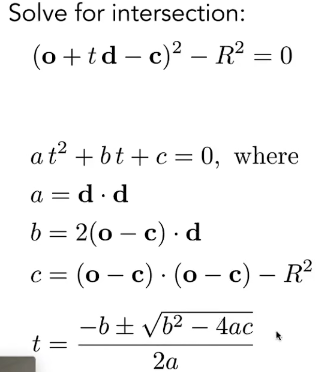
光线求交需要最近的点,在确保t是有意义的后,选取最小的t就是光线与求的交点
总结,光线与隐式表面求交方程
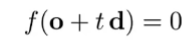
Ray intersection with triangle mesh(explicit显示表面)
封闭几何中,光线与几何交点数为奇数,则光线在三角内;否则在三角形外。
查看所有三角形是否与光线有交点。
将求交问题分解成两个
- 如何让光线与平面求交
- 交点是否在三角形内(已知)
问题聚焦到如何求光线与平面交点。
用一条法线+一个点定义一个平面。接下来只用判断交点连线已知点得到的向量与法线的关系。
设平面上已知一点p’,p为交点,N是法线向量。
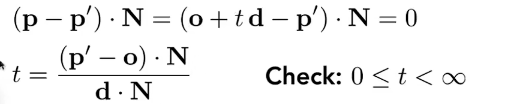
Moller Trumbore Algorithm
光线与三角形求交的另一个更快的方法。
【注意】这里有一个理解上的问题,也即是o+td到底是什么的问题。在一定时间范围内,它是一条射线;但是在某一个时刻,它是一个点。在计算中,我们考虑交点,其实也就是某一个时刻的角度来看。所以在涉及计算的时候,我们都是把它当作一个点来看。
与球求交时,把o+td当作交点来联立;上一个与三角形求交则是转换成了和平面求交,也是同理。
然后到了MT算法对三角形求交,通过观察下图,发现联立的表达式原本的点都变成了向量。所以可能存在理解上的障碍。
本来应该为o+t * D(vec) = (1-b1 - b2)P0 + b1 P1 + b2P2
其实观察发现这两个式子是等价的。
之前提到过,点的重心坐标中α,β,γ均大于0且相加等于1,那么点在三角形内。
通过克莱姆法则求解
Accelerating Ray-Surface Intersection(加速求交)
求交的简单方式: 光线遍历所有物体,找到最近的点
naive algorithm : pixel x object x bounce,计算量太大,很慢
如果使用Bounding Volume(包围盒,包围体),好处是能够筛掉连包围盒都不相交的物体,极大地剪枝。

我们经常使用的包围盒是Axis-Aligned Bounding Box(AABB,轴对齐包围盒),好处是与轴平行,便于计算光线与平面求交。三维情况下理解成三个对面(slabs)包围而成。
如何判断与盒子相不相交(二维与三维类似,下图为二维)
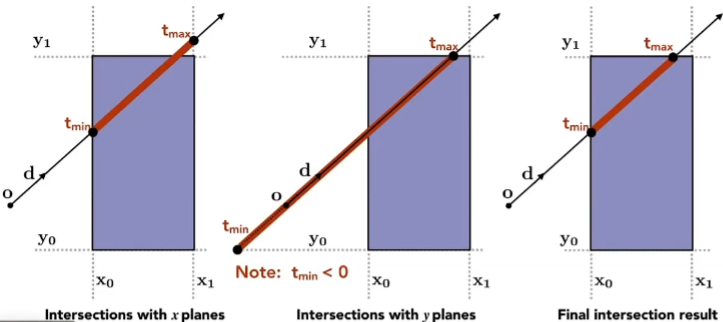
包围盒中对面(pairs of slabs) 全部进入才能算进入,只要有一个对面出去了,就算出去了。
核心ideas:(选取进入时间的最大时间,出去时间的最小时间)

结论
t(exit) > t(enter) >=0 在包围盒中呆过一段时间, 有交点(入和出)
t(exit) < 0,包围盒在光线反向延长的背后,由于是射线,所以不可能有交点。
t(enter) < 0,t(exit) >= 0,说明光线光源就在盒子里,有交点(只有出)
综上,当t(exit) > 0 && t(exit) > t(enter) 有交点。
我们已经知道包围盒的用处和用法了
那么如何具体地用AABB包围盒进行求交加速呢?
Uniform Grids(相同的格子)
Preprocess - Build Acceleration Grid(预处理-创建加速网格)
预处理指的是在光线追踪之前。
- Find bounding box(找到整个场景的包围盒,将所有物体包围)
- Create grid(设计合适的分辨率来创建网格,划分包围盒)
- Store each object in overlapping cells(标记相交的小盒子,储存起来)
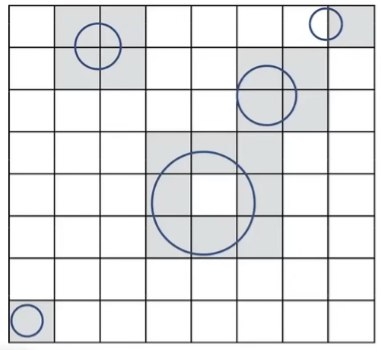
光线与盒子求交视为简单操作,当盒子中有物体,再与物体求交,没有则进入下一个盒子。
【问题】那么如何知道光线下一个进入的盒子是哪个呢?
这与光栅化一条直线类似(有确定的算法实现)。一个思路是光线从左下角射出,就只用判断右上的临近网格是否有交点。这样就能判断下一个盒子。
这种算法在Teapot in a stadium 的问题中,效果并不好,场景很大很不均匀,想要找到一个茶壶会很麻烦。求交就会变得很困难。
Spatial partitions(空间划分)
Examples
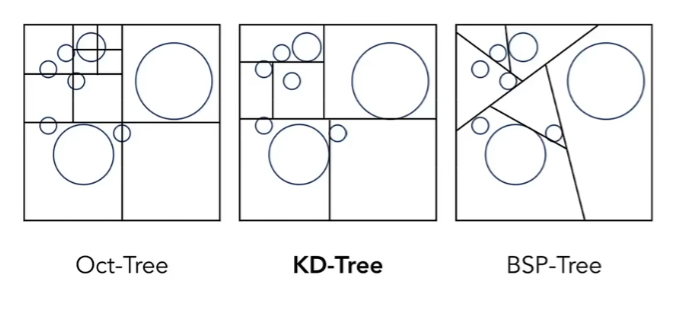
从左到右(represented with 2d, but both in 2d and 3d)
- 八叉树(每个维度切成2份,下图为二维状态,是四叉树),与维度呈2的指数幂,不是很理想。
- KD-Tree 类似于二叉树(x,y交替切分),一个格子切一刀,递归
- BSP-Tree 每个空间(非横平竖直地)划分一次
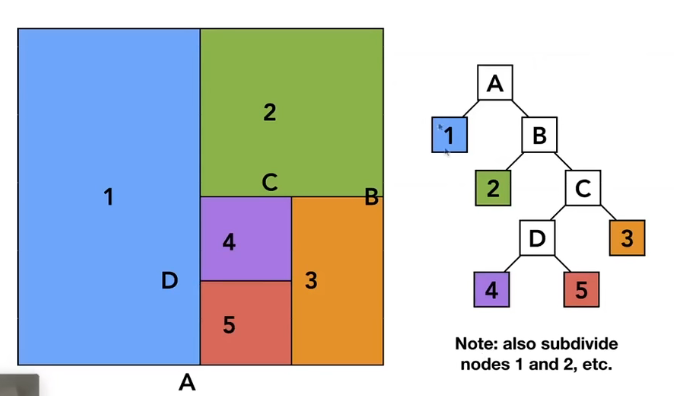
KD-Tree预处理Pre-Processing
【注意】
- 划分要沿着x,y,z轴(split axis)
- 划分位置不限,一般是在中点。
- 数据结构是二叉树,只有叶子节点才有数据
具体判断是否有交点的流程:
- 和left有交点,发现left是叶子节点,对left中所有物体进行求交,return;如果left不是叶子节点,进一步往下走,直到叶子节点位置。
- 然后查看right,同样的道理。
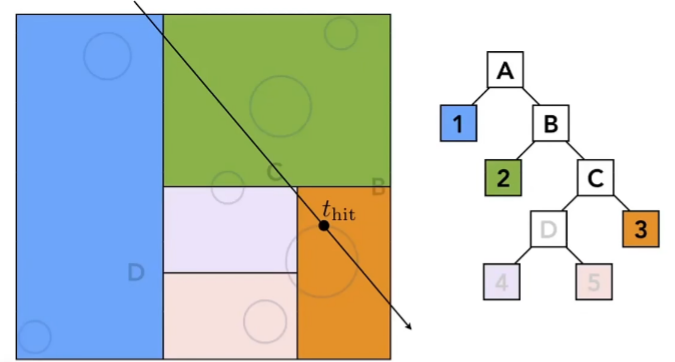
局限性
KD-Tree会出现一个几何结构,被拆分到多个叶子节点里,划分本身是单纯的直线切割,难免会拆分原来的几何。
因为需要对指定包围盒中的所有物体进行求交,但是KD-Tree判断三角形是否与AABB的包围盒有交点很困难,因为顶点不在包围盒里,也有可能有交点。近年间不太使用这个方法。
Object partition & Bounding Volume Hierarchy(物体划分和BVH)
上述两种划分方法都有一定局限性。
而BVH很好的解决了一些问题。BVH是一种得到非常广泛运用的方法。
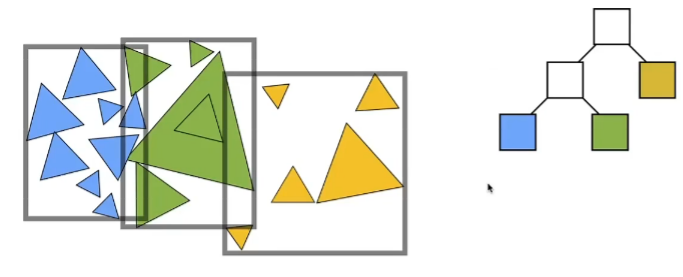
BVH划分包围盒是以物体为单位进行划分,不需要考虑三角形与物体求交,结构依旧是二叉树。
BVH的划分很有讲究,需要保证重叠部分尽可能少。
总结:先找包围盒,然后递归地分成两个子集,计算子集地包围盒。当叶子节点的三角形足够少就可以停止了。
最后储存叶子节点的数据。

划分的方法 Heuristic
优先选长轴开始划分,优先划分中间物体,保证左右平衡。
划分顺序是一个选择的过程。

Whitted风格的光线追踪到此为止




