Geometry(几何)
Introduce to Geometry
Examples of Geometry
机械

水

毛发

Representation of Geometry
Implicit(隐式表达)

隐式表达,一般看表达式,但是光看表达式并不直观。algebraic方式。
另一种方法是constructive solid geometry(csg,构造立体几何法)

距离函数Distance Function
希望blend得到AB的中间状态,SDF是有向距离场
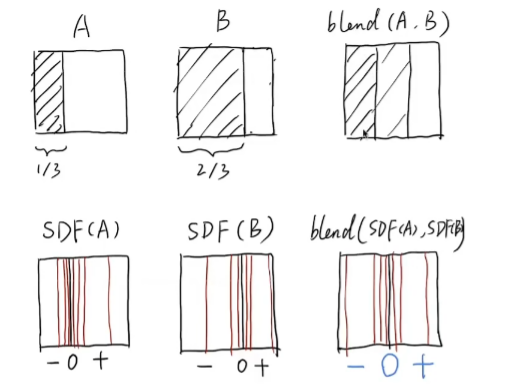
如果是第一行的图,结果不能得到左黑右白的中间态
第二行使用SDF,通过blend,可以得到0的位置,颜色围绕0开始渐变。
插值得到的SDF再转回原图像

Explicit(显式表达)
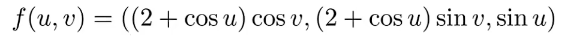
直接通过uv映射方式定义
隐式不知道函数的结果是哪个变量,显示知道;显示通过已知的自变量就能得出图形的结果样子。
Geometry is hard!
Point Cloud(最简单),lists of point,点足够多就成了面
Polygon Mesh(多边形网格),如三角网格
The Wavefront Object File(.obj) Format,这种.obj文件不是目标文件,而是一种文本格式,记录了顶点(vertices),法线(normal),纹理(texture),坐标(coordinates)
还有它们的connectivities;本质上就是一个3d白模文件。
Curve(曲线)
以上讲了两种几何的两种表达方式。接下来主要学习曲线这种几何的实现与应用。
贝塞尔曲线
类似于ps钢笔工具,选择控制点,帮助绘制曲线(显示表达)
如何绘制贝塞尔曲线?
de Casteljau Algorithm
举例:要求从b0开始,b2结束,t是时间记为【0,1】,共计三个控制点,如下图
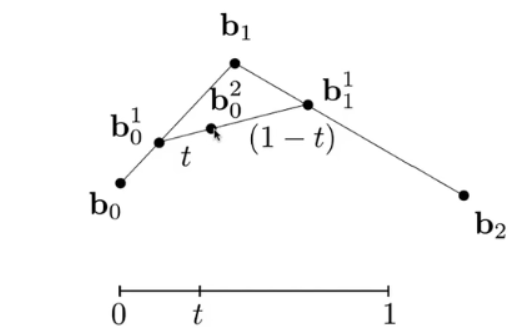
以时间t为单位进行划分,得到b01,b11,连线后再划分,recursively直到无法划分
最后我们得到曲线过三个点。

更普遍地
两个控制点画直线
三个控制点,绘制二次贝塞尔曲线。
…
若干个无限递归下去,n个点逐渐递归成一个点,不难发现(1-t + t) ^n的展开项正是控制点bj的权重
称之为伯因斯坦多项式,以下是n阶贝塞尔曲线的解析式
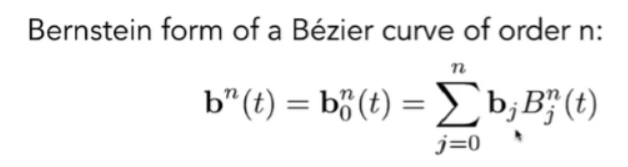
有关贝塞尔曲线的性质,1. 起点终点都固定 2.初始方向,最后方向确定 3. affine property仿射性质,想要移动变换曲线可以通过变换控制点。
4.凸包性质(Convex Hull):
想象蓝色线条为橡皮筋,橡皮筋包围的区域就是凸包
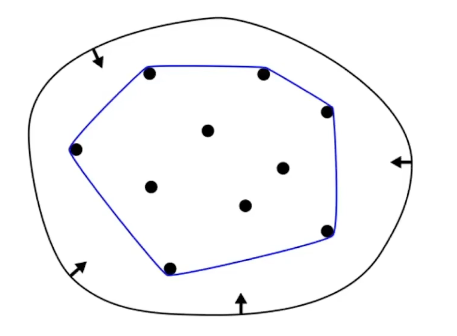
贝塞尔曲线一定在凸包里面
【补充】
- 二项展开:
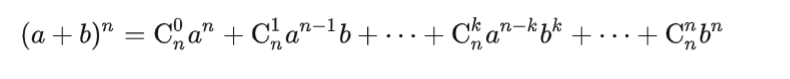
简记为:
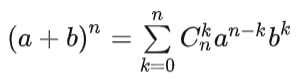
莱布尼兹多项式展开
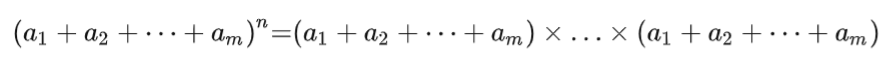
展开通项为(又叫做多项式定理)
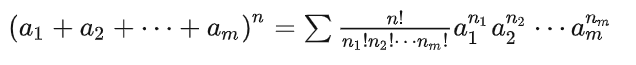
伯因斯坦多项式
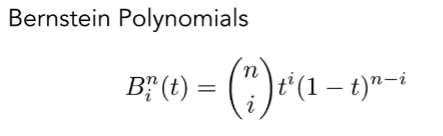
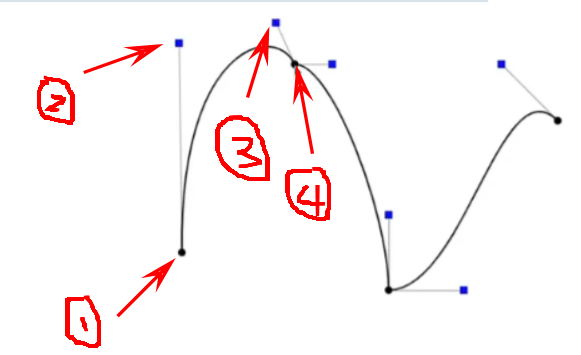
Piecewise Bezier(逐段贝塞尔)
多段3阶贝塞尔的连接。
示意图,曲线要连续,最后两个点决定终点导数,如果终点导数和下一个起点导数相等(蓝色标记共线等长),则认为曲线光滑连续。
【补充】
Spline 样条
有多个控制点,保持连续。一个可控的曲线。
用的多的有B-Spline(复杂度高)
Surface(曲面)
如何用贝塞尔曲线拓展到曲面,下图中,有一个4x4=16控制点的几何。
一共有四行,每行一条3阶贝塞尔曲线,只要控制贝塞尔曲线的高度,进而就能控制面的形状。
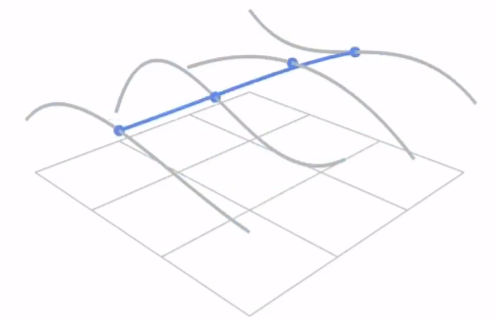
具体操作如下图,其实上述有一个问题,竖轴(假设贝塞尔曲线所在轴)可以随意控制,但是横轴的变形却未提及
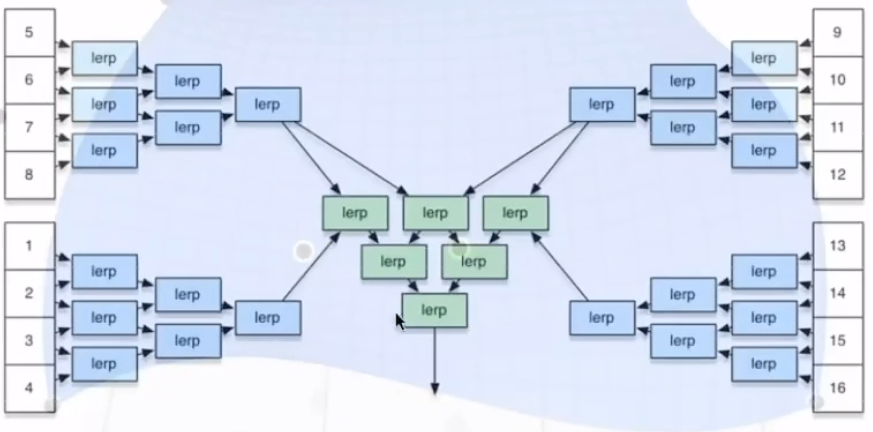
根据上图我们可以发现,四条贝塞尔分别插值,最后得到4个点再做二维的插值。由此可以实现贝塞尔曲面。
设参数为(u,v),横轴和竖轴的时间参数。显然这里也验证了贝塞尔曲线是显示的表达方式。
Mesh Operations(Geometry Processing)
Mesh subdivision(网格细分)
什么是细分?
可以理解为提高模型网格的精度(分辨率)

如何细分?
- 创建更多三角形
- 调整三角形的位置
Loop Subdivision
循环细分,拿一个三角形来举例,首先分成4个小三角形,然后调整位置。
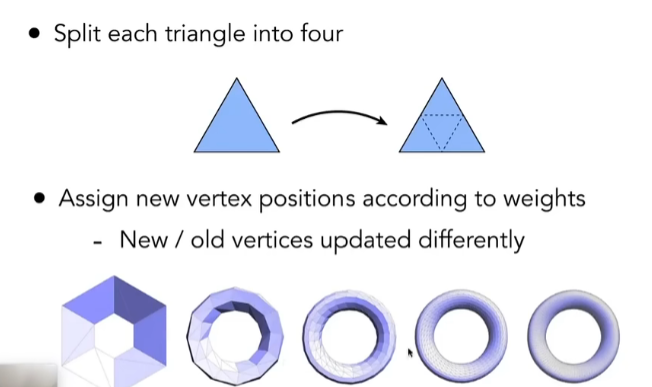
具体如何tune position(调整位置)呢?
- 得到的新顶点会根据与老顶点相对位置进行加权平均,如下图
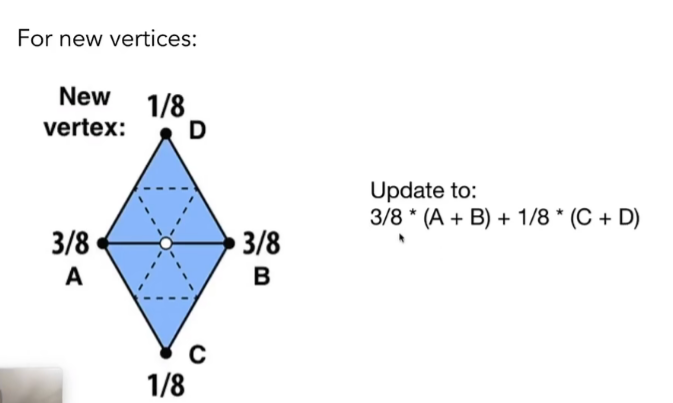
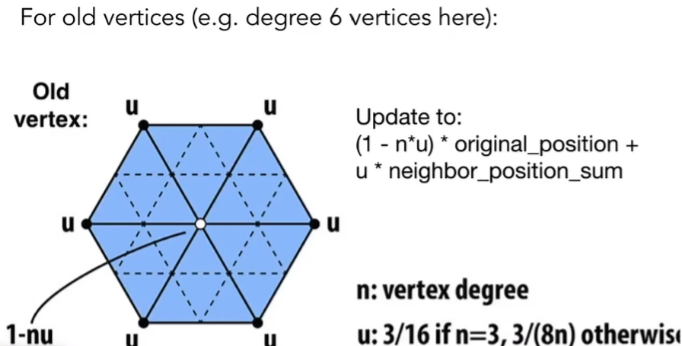
原来的**老顶点(old vertices)**也会进行一定程度的调整,其中n是degree,下图对于中间的白点,
由于度为6,连接了多个三角形,重要性相对就会比较低(n越大,白点的权重越小);同时邻点权重会变大。
Catmull-Clark Subdivision
使用Loop subdivision的条件是网格为三角形。但是如果网格为下图这样的情况。
Catmull-Clark可以用作不同形状的面。
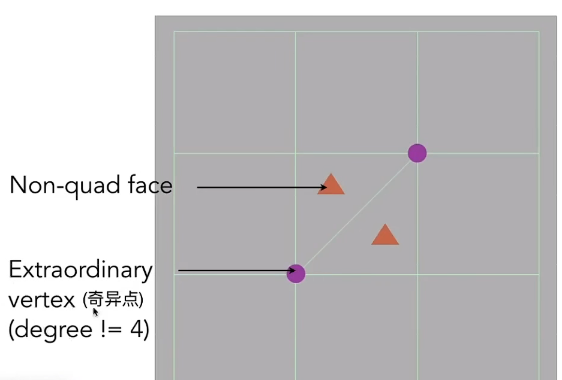
【条件】extraordinary vertices(定义度为不等于4的点为奇异点)
下图中,将边的中点连接交会到一个新的点(注意这个新的点同时也是面的中心);最后得到的两个新点再连接。发现已经没有三角形了。
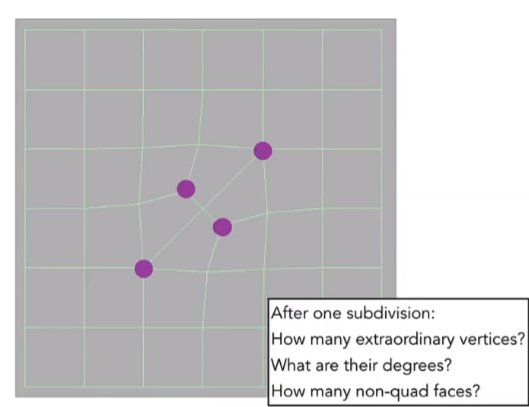
再细分多次
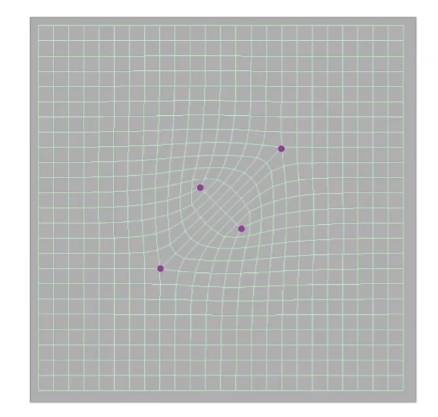
Catmull-Clark细分方法总结,1. 增加图元的方法是通过连接中点和图元中心 2.调整顶点位置(tune position)的方法依然是通过加权平均得到。图元中心为f,边的中点为e,图元顶点为v。

Mesh simplification
减少mesh图元的同时不改变形状
下图为不同数量三角面的结果。类似于mipmap不同层级用不同图片。
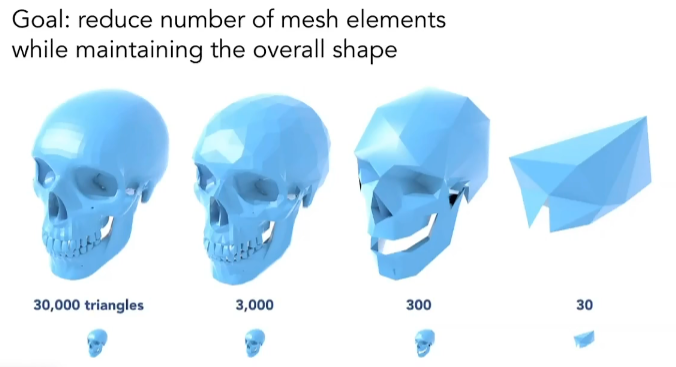
如何做网格简化
边坍缩
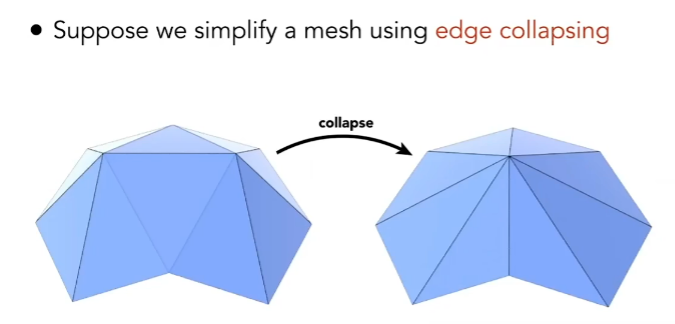
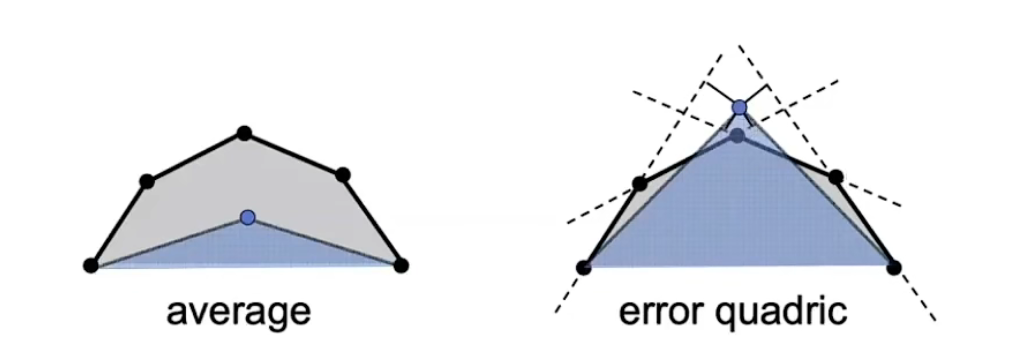
Quadric Error Metric(二次误差度量)实现边坍缩,下图中,我们需要将上面三个顶点坍缩成一个蓝色点。
需要找到一个最小的蓝点,使得该点(边)到其他三个点(面)的距离平方和最小。这个平方和就是二次度量误差,新建优先队列,将最小的误差放在前面,每次坍缩最小的那个。