Rasterization(光栅化)
Rasterization(光栅化)
前一节讲了变换(transform),过程总览如下图
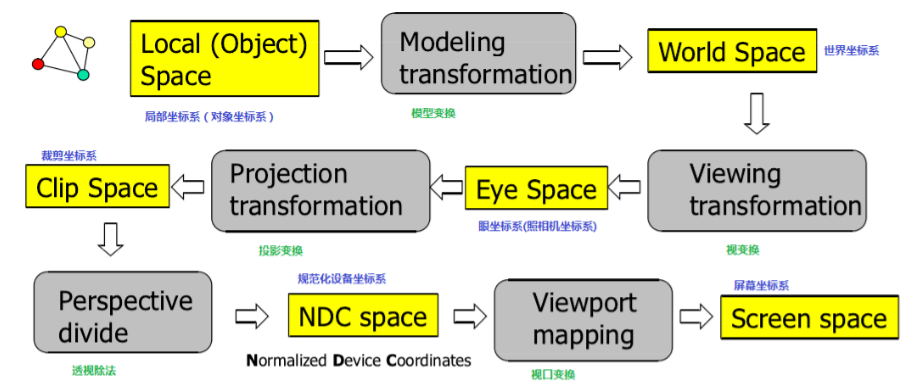
光栅化流程
之前提到了MVP过程,在这之后,所有的物体都会停留在【-1,1】^3
立方体(Canonical Cube)空间中,然后要进行光栅化。
Viewport Transformation(视口变换)
也就是将物体“画”到屏幕上,这里具体要做的是上图中的viewport mapping
即将【-1,1】拉伸(重映射remapping)到【width,height】的屏幕上
设置什么样的变换矩阵才能变换成功呢?
(其实在半兰伯特光照模型中就有这个思路,先乘以1/2,然后加上1/2,就转换到【0,1】区间了。)
根据这个思路得到转换矩阵
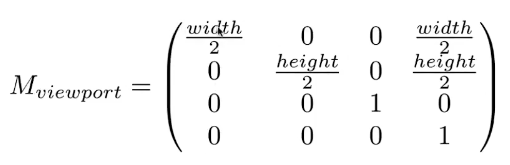
需要注意:这个变换与z值无关
Rasterizing triangles into pixels
上面只是说了光栅化是画物体到屏幕,具体来说,物体是由一个又一个多边形构成,最基本的元素是三角形,我们要做的是让这个三角行用像素画出来(或填充),进而在屏幕上显示。
具体实现算法就是通过遍历像素,判断像素中心是否在三角形内。
如何判断是否在三角形内
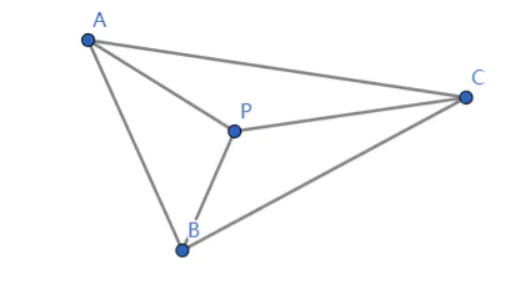
假设从ABC逆时针方向来看,
我们发现一个规律,但凡P点在三角形内,一定满足
n1 = AB x AP
n2 = BC x BP
n3 = CA x CP
三个方向都是朝着纸面向上,也就是说z分量大于0(充要条件),否则,则不在三角形内。
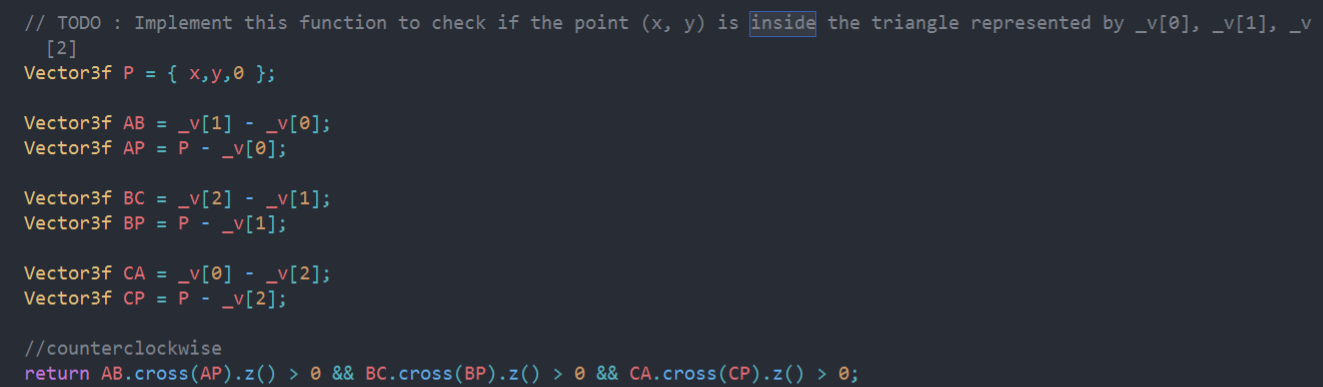
这样就可以判断是否在三角形内
另外遍历像素很麻烦,这里引入包围盒(Bounding Box)
引入axis-aligned bounding box(AABB)轴对齐包围盒
每一行都根据三角形边界用一个包围盒,这样就不会浪费,从而实现光栅化的加速。
但是并不简单。
在这里如果要单纯光栅化一个三角形,我们只知道三个顶点的坐标,这里可以粗略地将三角形用方形框住,只遍历方形中的像素。
光栅化细节之反走样
如果只是按照上述流程,结果其实并不理想。
最明显的就是,像素是方形,那么填充三角形会产生锯齿Jaggies
Aliasing(走样)
sample artifacts,采样所造成的瑕疵
- Jaggies(锯齿)
- Moire (摩尔纹)
- Wagon Wheel Illusion(车轮效应) 时间上采样的问题
信号变化太快,采样跟不上
如何反走样?(Antialiasing Ideas)
卷积、时域、频域、空间域和滤波
- 首先:这里用信号的方式表示反走样如下图,不同的函数,相同的采样点,采样结果却一样,导致不同信号无法区分,于是产生了走样
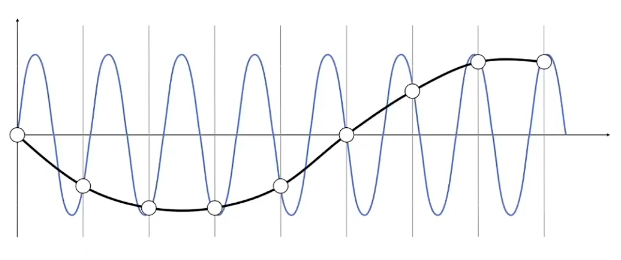
反走样的方法是Blurring:采样前做滤波(pre-filtering),什么是滤波?抹除特定的频率。
滤波 = 卷积 = 平均,顺序不能反先滤波后采样,不然不过是将走样后的图像再模糊了一下,还是走样的。
什么是卷积、时域、频域?
下图说明了卷积的过程,特定的卷积核对信号本身进行加权操作
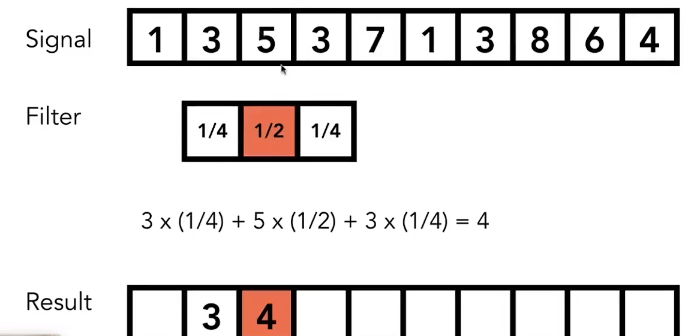
时域(time domain)自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t)是描述信号在不同时刻取值的函数。
频域(frequency domain)自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。
空间域(spatial domain) 简称空域,又称图像空间(image space),一般这个概念会出现在数字图像处理中,指由图像像元组成的空间。在图像空间中以长度(距离)为自变量直接对像元值进行处理称为空间域处理。
Fourier Transform(傅里叶变换)
傅里叶变换能做什么?将信号从时域转换到频域(对于一张图像,时域指不同空间的信号?;频域指的是信号随频率变化的函数)
傅里叶展开:任何周期函数都可以写成正弦余弦和的函数
傅里叶变换和逆傅里叶变换,将不同的函数之间相互转换
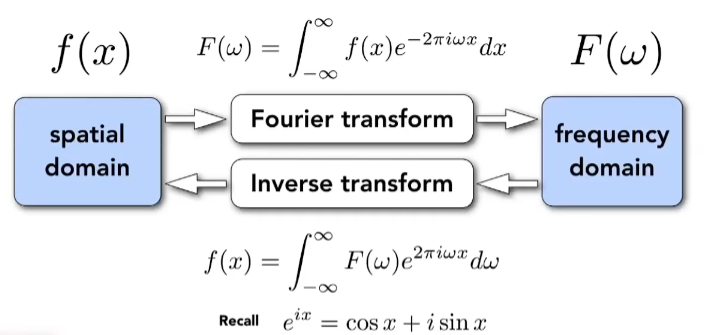
如以下例子

首先确定信号变换时一般都是默认为周期性函数,但是对于非周期性的图像,则会水平竖直平铺多张图像,
边界变化剧烈,于是有了两条白线。
任何信号在不同频率的样子叫做频谱。
下图为高通
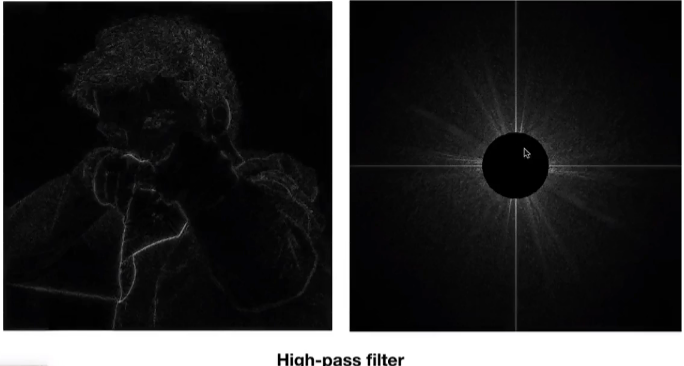
下图为低通

下图为高低频都去掉的结果(中通滤波)

Convolution Theorem(卷积定理)
spatial domain上的卷积(平均)模糊等价于
frequency domain上的乘积
时域的卷积等于频域的乘积(暂时不清楚spatial domain和time domain的区别)
尤其注意,卷积定理有两个,时域的乘积 也等于 频域的卷积,对偶性(详情查询)
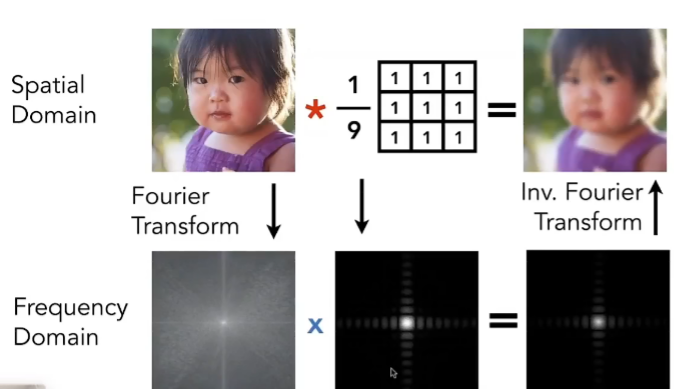
上图的卷积核,也叫做滤波器,由于上图将低频信息保存了下来,也叫做低通滤波器low box filter
越大的box结果越模糊。
走样现象的另一种解释
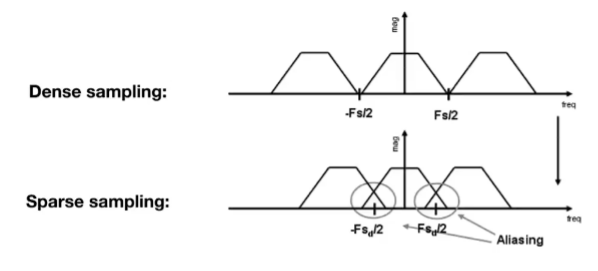
像素很大,采样很稀疏,频谱密集
采样速度不够快,导致频谱混叠,信息损失,造成走样
归纳反走样或减少走样方法
Increase sample rate(reduce aliasing error)
先模糊后反走样,先低通,后采样,高频滤掉,就不会产生重叠;
关键点在于,频谱混叠导致结果失真,但是模糊只会丢掉高频细节。后者显然更好
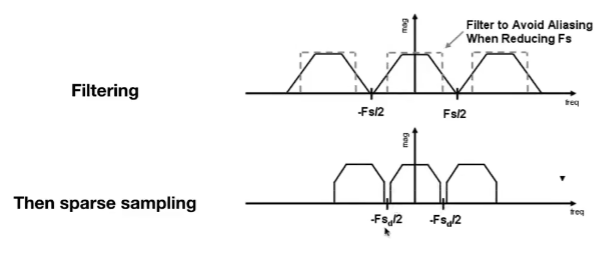
实际应用中的反走样
MSAA(Multi Sample Anti-Aliasing)
将一个像素分成多个“小像素”
如4x4
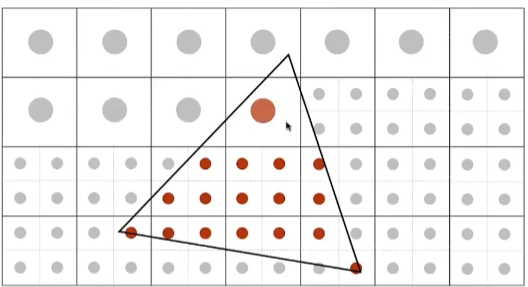
根据小像素覆盖率来进行模糊,这样能够更准确的确定模糊度,然后采样
注意:MSAA并不是通过提高分辨率真的增加”小像素“,只不过是在一个像素里采样若干个点
但是上述例子的代价是增加了4x4共16倍的采样量
另外还有FXAA(后处理,得到锯齿才处理)和TAA等方法




