Transformation(变换)
Transformation(变换)
变换的数学意义(介绍)
Why Transformation
Q1: 为什么要学习变换呢?
A1: 动画的实现,光栅化图像变换投射进“人眼”。由于计算机最终的变换服务于数学世界,于是同一用矩阵来表示变换,线性代数中学过对应知识。
Q2: 举例有哪些变换?
A2: Scale Matrix,缩放;Reflection Matrix,对称(镜像);
Shear Matrix,切变(有称”错切“,”斜切“);
Rotate Matrix…
旋转矩阵推导
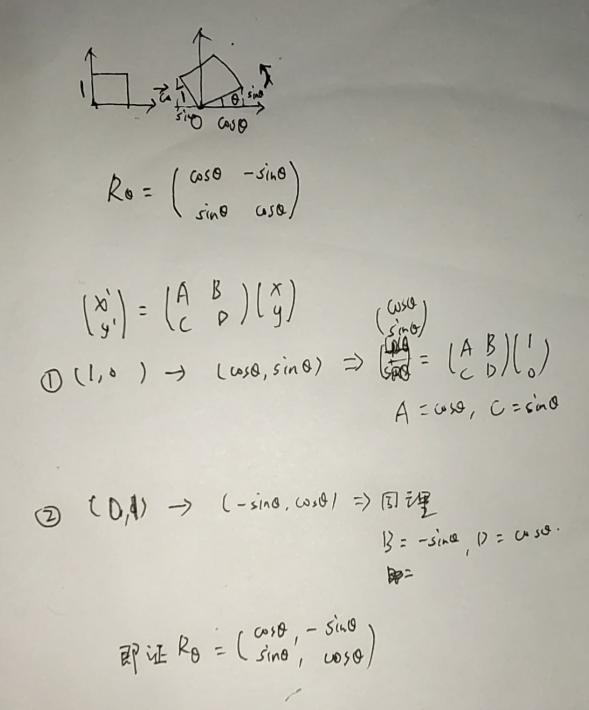
到目前为止的变换,我们都可以对(x,y…)进行线性变换(Liner transformation)得到变换结果(x’,y’)
但是平移变换不行?
试想一下,如果对x平移一个单位,那么变换矩阵
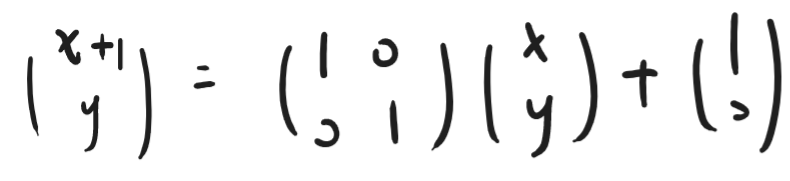
无法用一个矩阵就解决变换,(上面的变换形式引出仿射变换(Affine Transformation)的概念),同时进行线性和平移变换
接下来
Homogeneous coordinates(齐次坐标)
要想用一个矩阵表示所有变换
这里引入了齐次坐标的概念,以二维举例,引入第三维度
设点的第三维度为1,向量为0.
- 之所以向量为0,是因为向量具有方向不变性,假设进行平移变换,我们希望这个向量前后不变的;但是如果但三维度不是0,那么结果就有可能出现向量方向的变化。
- 之所以点为1,是因为这样就解决了平移问题,通过增加维度,使得一个矩阵同时表示平移和线性变换。
另外

在齐次坐标系下,不难推导出,点+点等于中点,只需同时除以w=2,使得w回归为1
最后放一张仿射变换的图片和常见变换公式的图片
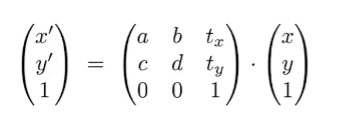

Composing Transform(变换组合)
我们需要知道,复杂的一连串的变换是可以组合的,因为虽然变换越多,矩阵越多,但是由于都是乘法,根据矩阵结合律可以最终合成一个
平移和旋转具有严格先后顺序,毕竟先加后乘,与先乘后加结果不一样;具体来说是先乘后加,先变换后平移
Decomposing complex transform(解构复杂变换)
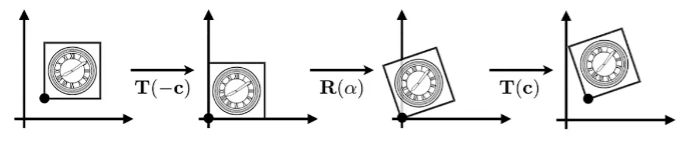
由图知,直接从图一到图四其实并不方便。
我们先把物体的旋转中心移平移回原点,然后旋转,最后平移回去。(因为我们只能做原点为旋转中心的旋转,不然就无法用之前的固定结论)。
如果不以原点为旋转中心,以某个轴为旋转中心轴
绕z轴旋转(本来二维的扩展成三维后等价绕z轴旋转)
- 绕哪个轴,哪个轴的坐标为位置不变
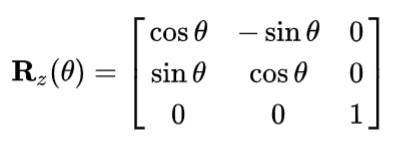
拓展到3d transformation也是一样
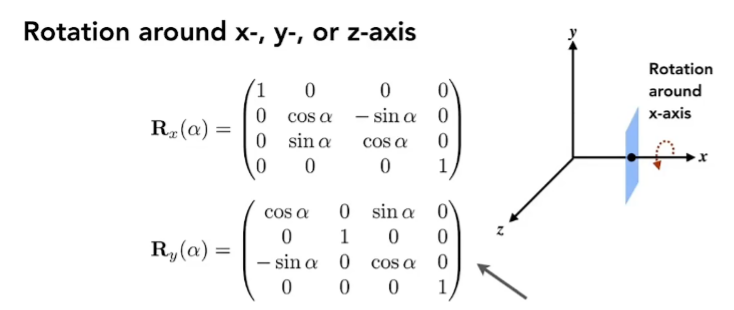
ps: 按照直觉可能会觉得绕y轴的旋转矩阵有问题,其实是因为该图表示的是右手坐标系的变换;已知x.crossproduct(z) = -z.crossproduct(x)(右手法则),这里XxZ = -Y,所以需要对α取反。
Rodrigues’s Rotation Formula
描述了绕任意轴旋转任意角度的变换矩阵
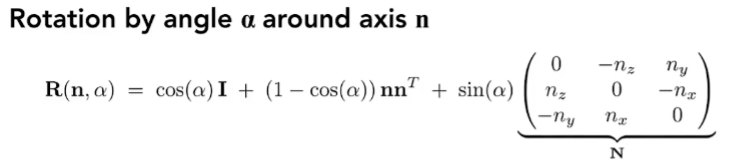
下面来推导一下这个公式同时引入四元数的学习
参考:四元数和旋转(Quaternion & rotation) (zhihu.com)
前提:axis n是一个单位向量,并且n过原点(如果不过原点,参考前面的方法先平移回原点)

有关四元数
定义:

MVP Transformation(实际操作)
拍照过程
- 摆放好待拍摄的物品,或者人物。(model transformation)
- 调整好拍摄(相机)角度。(view transformation)
- 调整焦距,拍摄。(projection transformation)
也就是常说的MVP变换
这里Viewing Transformation包括了View Transformation(视图变换)和Projection Transformation(投影变换)
View/Camera Transformation(视图变换)
视图变换就是把相机放好。把相机移回原点,相机的三个向量分别和世界坐标的三个轴对齐。先平移后旋转
- 平移回原点
- 旋转对齐轴
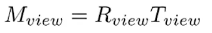
平移矩阵很好得到
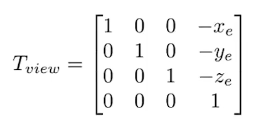
然后是旋转矩阵
但是要想将相机三向量t,g,x转换到世界坐标轴XYZ(单位向量)上,其实不好算,所以这里反过来算
所以首先明确目标矩阵(1 0 0 0;0 1 0 0; 0 0 1 0; 0 0 0 1),由于反过来算,所以变成了起始矩阵
细节: g to -Z,相机对准Z的负方向,t to Y, gxt to X,x由g、t叉乘得到
R(view)的逆矩阵很好得到,毕竟(0,0,1)旋转到一个位置很好做
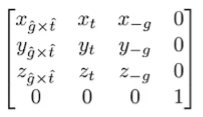
至此实现了从世界坐标轴到相机坐标轴的旋转,只要额外再取个逆,就能得到R(view)
Projection Transformation
Orthographic projection
正交投影假设物体和相机无限远,这样物体通过视锥体投影到相机没有近大远小
以下这张图解释了这个过程(先平移后缩放)
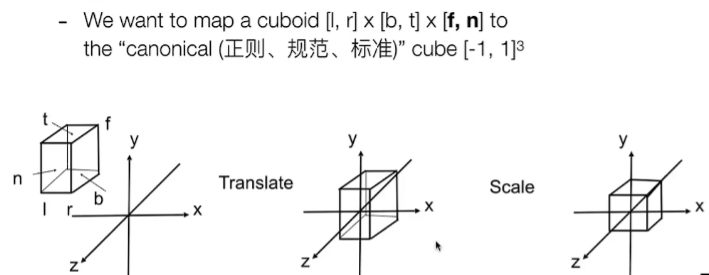
注意:这里是右手系,相机往-z方向看,OpenGL就是右手坐标系。
但是unity 和 dx都是左手坐标系
再这样的前提下|f|要比|n|要小
由此得到正交变换的变换矩阵
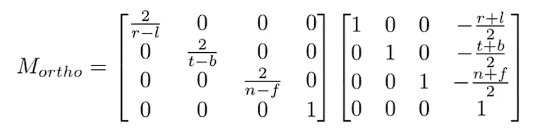
如何理解r,l,b,n,f,t这些东西,可以理解成物体左右上下前后的“坐标”,
平移矩阵好理解,缩放矩阵本质上是用【2/左右距离】作为缩放倍数,最后结果为2,使得物体缩放到【-1,1】的cube中。
至此正交投影结束
Perspective projection
视锥体原平面投影到近平面就能产生透视效果
这里做透视投影的过程是,先将视锥体squish(挤)成cuboid(长方体)再做正交投影
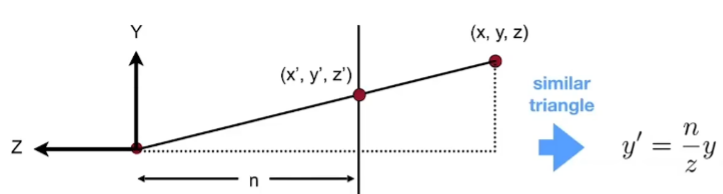
由远近平面的关系,我们可以根据相似三角形得到比例关系
y' = (n/z)y
首先明确我们的目标是将(x,y,z)变换到(x’,y’,z’)
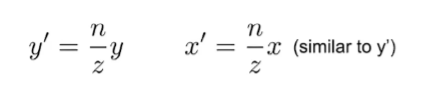
进而在齐次坐标上是
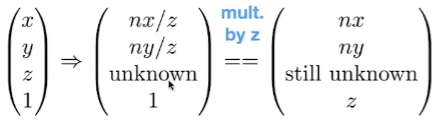
从透视投影到正交投影的矩阵可以写成
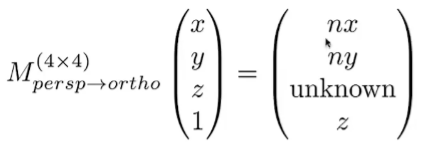
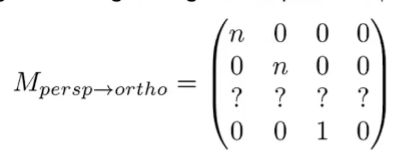
这里我们要具体推导一下第三行的值
本质上就是用远近平面上的点带入,完成二元方程组,进而推导出第三行

最后合成透视矩阵
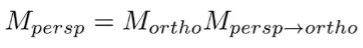
推导结束
至此,坐标被变换到了Clip Space(裁剪空间),也称作Projection Space(投影空间)
这块空间用于裁剪掉不需要的内容,使用视锥体(view frustum)




