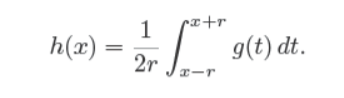No title
Signal Processing
在图形中,我们经常要处理具有连续变量的函数:一开始你只看到一张图像,但是随着你的探索,你将会看到更多。本质上,连续函数不能直接在电脑上表达,我们必须用优先的比特来表达他们。
最有用的方法之一是存储这个函数在不同点的值,然后在需要的时候进行重构。
你现在位置应该熟悉使用二维网格像素来表达图像,所以你已经见过一个采样的表现。
另一个关于sampled representation 的粒子是二维的数字化平板。
例如平板电脑,或者艺术家使用的数位屏。这种情况下,最原式的函数是数位笔的移动
(stylus数位笔触针手写笔)
…
Digital Audio : Sample in 1d
即使sampled representation 已经用于电子交流很久了,激光唱片(compact disc)在1982年的引入,紧随着音频数字记录器的使用增长,在过去的10年里,是第一个高度可视的消费者应用采样。
…
Sampling Artifacts and Aliasing
数字音频记录可以为sampling 和reconstruction处理更加具体的模型。
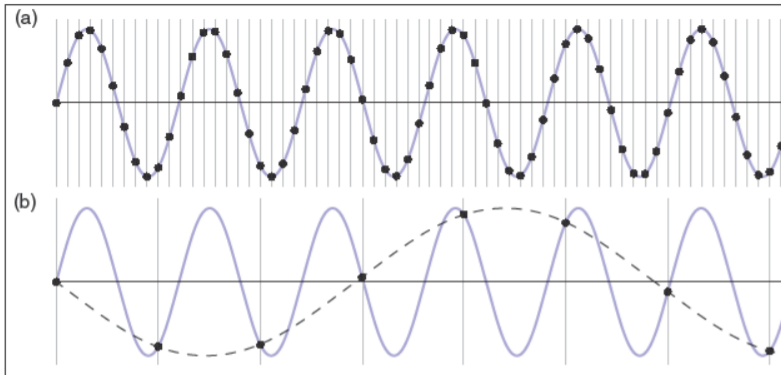
Aliasing 展示了不管什么时候,采样重构失效导致人工结果是一个令人惊讶的频率
在音频中,走样以一种奇怪的声音和额外的声调–一个10Hz的bell ring,当采样到8Hz,就变成一个6Hzd的声调
在图像中,走样经常因为采样网格的interaction和图像中常规特点。以moire pattern的形式出现。
Convolution
在我们讨论sampling和reconstruction算法之前,我们首先要检验它们基于的数学该奶奶
convolution卷积。
卷积是一个简单的数学概念,为算法作基础用来采样,过滤,重构。
同时它也是我们如何分析这些算法的基础。
卷积是一个function:它使用两个functions,然后将它们结合成一个新的function
这本书中,卷积运算符用一个*标记。f * g,f is convolved with g
卷积可以被用于连续方法或者离散的序列。
同时也可以被用于定义在1d,2d,3d或者更高维度.
为了定义方便,我们通常假设函数定义域区域无限。

Moving Average
为了得到一个基础的卷积图像。
思考:使用moving average来平滑一个函数。
为了在任意一个点得到平滑的值,我们需要计算函数超出范围拓展到每个方向,距离长度为r 的平均值。
距离r是平滑的radius,控制平滑度
我们用数学方法表示,如果平滑一个连续的函数g(x),平均化(averaging)意味着在区间内对g进行求积分
(integrating)