Computer Graphics 05
Viewing
Viewing Transformations
视角变换用于映射3d位置。
它是一头复杂的野兽,依赖于包括相机坐标、orientation(取向),投影的类型,视角的区域,和图片的清晰度(resolution);
它是通过几个简单变换点乘获得
- 相机变换(camera/eye transformation)
- 投影变换(projection transformation)
- 视口(窗口)变换(viewport transformation)
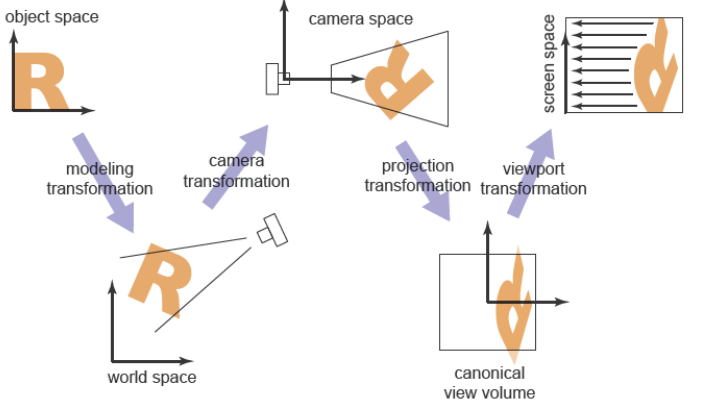
模型空间->世界空间->相机空间->规范化视线空间->屏幕空间
The Viewport Transformation
假设我们想要看到的几何体在规范的视图体积空间(canonical view volume)
然后我们想要在z轴方向用**正交(orthographic)**相机观察
canonical view volume(规范视图空间)是一个包含了所有3d坐标的正方体,这些坐标
在笛卡尔坐标系(cartesian coordinates)中处于(-1,1)之间
我们将x = -1投射到屏幕的左边,y = -1投射到屏幕的底部,像素坐标的定义是围绕着
以整数坐标为中心的方形。这样图像的边缘就有半个unit的overshoot
如果我们想要在图片上画nx * ny个像素,我们需要将square[-1.1]映射到[-0.5,nx - 0.5]
x [-0.5,ny - 0.5]
这里是假设线段完全在规范视角空间里,后面会放下这个假设,讨论clipping(裁剪)
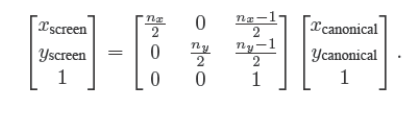
Xscreen = nx/2 * Xcanonical + (nx - 1) / 2
…
注意这个矩阵忽略了z分量,因为这不影响投影到图片,但是在正式称呼这个矩阵为视口矩阵
(transform to screen),我们需要增加一一行和一列来存储z分量,不改变z分量

最终这个投影到屏幕
The Orthographic Projection Transformation
当然,我们通常想要在除了canonical view volume空间的一些区域渲染几何体。我们的第一步是生成视图,这个视图保持view dir,orrientation不变,looking alone -z with +y up.
我们将在右边乘以另一个矩阵来增广这个矩阵。
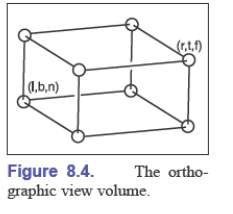
the six params are respectively left,right,bottom,top,near,far
正交视图空间是在-z轴上,所以f是更小的负数
在z轴上,这样近视图反而比远视图更大,这是非直觉性的(uninstuitive)
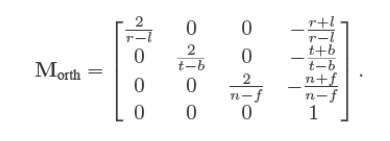
omit …..




